The switch Statement with the Arrow (->) Notation
The form of the switch statement with the arrow notation is shown in Figure 4.4. This form defines switch rules in which each case label is associated with a corresponding action using the arrow (->) notation.
Figure 4.4 Form of the switch Statement with the Arrow Notation

switch (
selector_expression
) {
// Switch block with switch rules defined using arrow notation:
case
CC
->
expression_statement
;
case
CC
1
,
CC
2
, …,
CC
m
->
block
case
CC
4
->
throw_statement
…
default -> …
}
Compared to the switch statement with the colon notation (Figure 4.2), there are a few things to note.
First, although the case labels (and the default label) are specified similarly, the arrow notation does not allow multiple case labels to be associated with a common action. However, the same result can be achieved by specifying a single case label with a list of case constants, thereby associating the case constants with a common action.
Second, the action that can be associated with the case labels in switch rules is restricted. The switch statement with the colon notation allows a group of statements, but the switch statement with the arrow notation only allows the following actions to be associated with case labels:
By far, the canonical action of a case label in a switch rule is an expression statement. Such an expression statement is always terminated by a semicolon (;). Typically, the value returned by the expression statement is discarded. In the examples below, what is important is the side effect of evaluating the expression statements.
…
case PASSED -> ++numbersPassed;
case FAILED -> ++numbersFailed;
…
A block of statements can be used if program logic should be refined.
…
case ALARM -> { soundTheAlarm();
callTheFireDepartment(); }
…
The switch rule below throws an exception when the value of the selector expression does not match any case constants:
…
default -> throw new IllegalArgumentException(“Not a valid value”);
…
Third, the execution of the switch rules is mutually exclusive (Figure 4.5). Once the action in the switch rule has completed execution, the execution of the switch statement terminates. This is illustrated in Figure 4.5 where only one expression statement is executed, after which the switch statement also terminates. There is no fall-through and the break statement is not necessary.
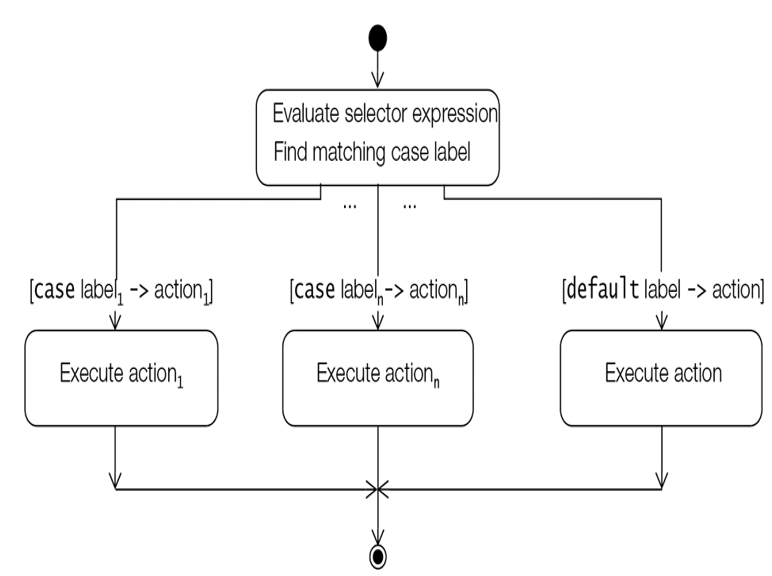
Figure 4.5 Activity Diagram for the switch Statement with the Arrow Notation
Example 4.3 is a refactoring of Example 4.2 with a switch statement with the arrow notation. At (2), (3), (4), and (8), the action executed is an expression statement, whereas at (5), the action executed is a block. Using switch rules results in compact and elegant code that also improves the readability of the switch statement.
Example 4.3 Nested switch Statements with the Arrow Notation
public class SeasonsII {
public static void main(String[] args) {
int monthNumber = 11;
switch(monthNumber) { // (1) Outer
case 12, 1, 2 -> System.out.println(“Snow in the winter.”); // (2)
case 3, 4, 5 -> System.out.println(“Green grass in the spring.”); // (3)
case 6, 7, 8 -> System.out.println(“Sunshine in the summer.”); // (4)
case 9, 10, 11 -> { // (5)
switch(monthNumber) { // Nested switch (6) Inner
case 10 -> System.out.println(“Halloween.”);
case 11 -> System.out.println(“Thanksgiving.”);
}
// Always printed for case constants 9, 10, 11:
System.out.println(“Yellow leaves in the fall.”); // (7)
}
default -> throw new IllegalArgumentException(monthNumber +
” is not a valid month.”);// (8)
}
}
}
Output from the program:
Thanksgiving.
Yellow leaves in the fall.